[Latest] All Mensuration Formula In Hindi PDF Download

पोस्ट के इस भाग मे, आपको Mensuration Formula In Hindi मे बताया गया है। आप मे से कई लोगों को कभी-कभी कुछ mensuration के formula ध्यान नहीं रहते। तो अगर ऐसा है, तो इस पोस्ट को पूरा जरूर देखें तथा इस पोस्ट मे दिये गये formula of mensuration PDF भी download करीए। जो आपके पास हमेशा रहेगी याद करने के लिए।

यहाँ नीचे मैने पूरी जानकारी mensuration से संबंधित दिया है, कि Mensuration kya hota hai, इसके कितने भाग है तथा किसका-किसका क्या सुत्र है। तो बस पुरी पोस्ट पढ़े इससे आपको काफी अच्छी जानकारी मिल जायेगी।

All Mensuration Formula In Hindi & English

Mensuration को हिंदी मे क्षेत्रमिति कहते है। इसके दो भाग है- 1) 2D, 2) 3D,

2D मे ये आकृतियाँ है-

• आयत (Rectangle)
• वृत (Circle)
• वर्ग (Square)
• Circle Ring Formula
• त्रिभुज (Triangle)

3D मे ये आकृतियाँ है-

• धन (Cube)
• धनाभ (Cuboid)
• शंकू (Cone)
• गोला (Sphere)
• बेलन (Cylinder)
• Hollow Cylinder Formula (खोखले बेलन)
• अर्धगोला (Hemi Sphere)
• खोखला गोला (Hollow Sphere)

2D Mensuration Formula Hindi & English

आयत (Rectangle Formula)

आयत के आमने-सामने के की भुजा बराबर होती है तथा इनके विकर्ण भी समान होते है। इसका प्रत्येक कोण 90 अंश का होता है।

• क्षेत्रफल (Area Of Rectangle)= लम्बाई × चैड़ाई (l×b)
• परिमिति (Perimeter)= 2(लम्बाई+चैड़ाई)
• विकर्ण (Diagonal) = √लम्बाई^2 × चैड़ाई^2

वृत्त (Formula For Circle)

एक बिंदु के परीतः खींचा गया बिंदुपथ वृत कहलाता है। इसकी दूरी चारो तरफ समान रहती है तथा जिस बिंदु के परीतः बिंदुपथ खींचा गया है वर वृत्त का केंद्र कहलाता है। केंद्र से बिंदुपथ की दूरी को त्रिज्या कहते है तथा वृत की परिधि से मिलने वाली दोनो तरफ की रेखा को व्यास कहते है। परिधि वृत्त को घेरने वाली रेखा होती है।

जो रेखा वृत के केन्द्र से होकर नहीं जाती, वह वृत की जीवा कहलाती है, तथा इसी जीवा द्वारा वृत के हुआ भाग को वृत खंड कहते है।

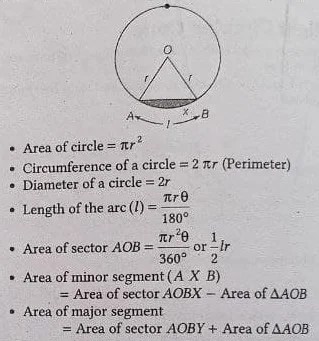
• वृत्त की त्रिज्या (Radius)- r
• व्यास (Diameter)- 2r
• वृत्त का क्षेत्रफल- πr^2
• वृत्त की परिधि- 2πr

वर्ग (Formula Of Square)

वर्ग की चारों भुजाएं समान होती है जिसे a से प्रदर्शित किया गया है तथा इसके विकर्ण भी समान होते है तथा एक-दूसरे को 90 अंश पर काटते है।

• वर्ग की भुजा= 2
• वर्ग का क्षेत्रफल= a^2 = 1/2 × विकर्ण
• वर्ग की परिधि= 4a
• वर्ग का विकर्ण (d) = a√2

Also See- Samas Kya Hai

Circle Ring Formula

यह आकृति एक प्रकार के गोलाकार घेरे के चारो तरफ बने नये रास्ते या फिर छल्ला की आकृति होती है।

• Area Of Circular Ring= π(R^2-r^2)

त्रिभुज (Triangle Formulae)

किन्ही तीन भुजाओं से बनी आकृति त्रिभुज कहलाती है तथा यह तीन कोण बनाती है। तीनो कोणों का मान सदौव 180 degree होता है। यहाँ मै आपको त्रिभुज के तीप प्रकार के बारे मे बातऊंगा सूत्र के साथ।

समबाहु त्रिभुज (Equilateral Triangle Formula)

जिस त्रिभुज की तीनो भुजाए समान होती है तथा प्रत्येक कोण 60 degree का होता है, वही समबाहु त्रिभुज कहलाता है।

• क्षेत्रफल= √3/4 × a^2
• अंतःवृत्त की त्रिज्या= a/2√3
• परिवृत्त की त्रिज्या= a/√3

समकोण त्रिभुज (Formula Of Right Angle Triangle)

जिस त्रिभुज का एक कोण 90 अंश को होता है वह समकोण त्रिभुज कहलाता है। इस त्रिभुज मे तीनो भुजा असान होती है। तथा लम्ब तथा आधार के वर्णों का योग का रूट कर्ण के बराबर होता है। इसे पाइथागोरस प्रमेय भी कहते है।

• समकोण त्रिभुज का क्षेत्रफल= 1/2 × आधार × लम्ब

विषमबाहु त्रिभुज (Asymmetrical Triangle Formula)

विषमबाहु त्रिभुज मे न ही प्रत्येक भुजा बराबर होती है और न ही तीनो कोण बराबर होते है।

• विषमबाहु त्रिभुज का क्षेत्रफल= √s(s-a)(s-b)(s-c)
• s= (a+b+c)/2

Also See-

• Important Days And Dates
• Vachan In Hindi

3D Mensuration Formula Hindi & English

घन का सूत्र ( Cube Formula)

यह एक त्रीविमिय आकृति है। इसमे तीन फलक होते है, जिसमे लम्बाई, चौड़ाई के साथ ऊँचाई भी होती है। घन मे सभी लम्बाई, चौड़ाई तथा ऊँचाई बराबर होती है। यह एक ठोस आकृति होती है।

• आयतन= a^3
• कुल पृष्ठीय क्षेत्रफल= 6a^2
• पार्श्वीय पृष्ठ क्षेत्रफल= 4a^2
• धन का विकर्ण (Cube Diagonal)= 2√3

धनाभ के सूत्र (Formula Of Cuboid)

धनाभ मे भी तीन फलक होते है, तथा ये तीनो फलको के मान अलग-अलग रहते है। यह भी एक 3D ठोस आकृति है। इसमे लम्बाई(L) , चौड़ाई(B) तथा ऊँचाई(H) होता है।

• घनाभ का आयतन= LBH
• घनाभ मे रखा सबसे लम्भा छड़ का सूत्र= √L^2+B^2+H^2
• घनाभ का कुल पृष्ठीय क्षेत्रफल= 2(LB+BH+HL)
• पार्श्वीय क्षेत्रफल या कमरे का क्षेत्रफल = 2(L+B)×H

गोला के सूत्र (Mensuration Formula Of Sphere)

यह भी एक 3D आकृति है, उदाहरण के लिए आप ठोस गेंद को Sphere मान सकते है। इसमे केन्द्र से स्तह तक की दूरी को r यानि त्रिज्या कहते है।

• गोले का आयतन= 4/3 πr^3
• गोले का वक्रपृष्ठ= 4πr^2

अर्द्ध गोला (Hemi Sphere Formula)

यह एक ठोस गोले का आधा कटा हुआ भाग होता है।

• Volume Of Hemisphere= 2/3πr^3

खोखला गोला (Hollow Sphere Formula)

इस आकृति को आप एक टेनिस के गेंद के समान समझ सकते है।

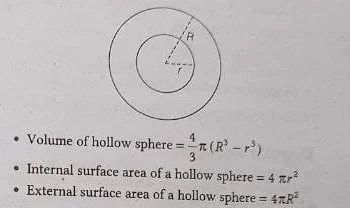
• Volume Of Hollow Sphere (खोखले गोले का आयतन)= 4/3 π(R^3-r^3)
• Internal Surface Area Of Hollow Sphere= 4πr^2
• External Surface Area Of Hollow Sphere= 4πR^2

बेलन का सूत्र (Cylinder Formula)

आयत को उसकी लम्बाई या चौड़ाई के अनुदिश घुमारे पर प्राप्त आकृति ही बेलन होता है। इसे आप घर के गैस के सिलेंडर से समक्ष सकते है। यह भी 3D आकृति है।

• Volume Of Cylinder (आयतन)= πr^2h
• TSA Of Cylinder (कुल पृष्ठीय क्षेत्रफल)= 2πr(h+r)
• CSA Of Cylinder= 2πrh

Hollow Cylinder Formula (खोखले बेलन का सुत्र)

यह एक प्राकर का बेलन होता है जो कि अन्दर से खोखला होता है। इसे आप पानी के पाइप से समझ सकते है।

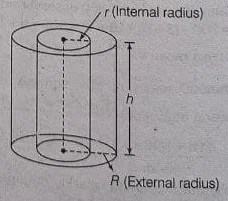
• Volume Of Hollow Cylinder (खोखले बेलन का आयतन)= πh (R^2-r^2)
• TSA or Total Surface Area Of Hollow Cylinder= 2πh(R+r) + 2π (R^2-r^2)
• CSA or Curved Surface Area Of Hollow Cylinder= 2πh (R+r)

शंकु के सूत्र (Cone Formula)

समकोण त्रिभुज को उसकी ऊंचाई के परितः घुमाने पर प्राप्त आकृति शंकु कहलाती है।

• Volume Of Cone= 1/3 πr^2h
• CSA Of Cone= πrl= πr √(r^2+h^2)
• Cone TSA= πr (l+r)
• Slant Height Of Cone= √(r^2+h^2)

All Mensuration Formula PDF Download

यहाँ आपको मैने download का लिंक दिया है, जिससे आप mensuration all formula को देख सकते है कभी-भी, इसमे मैने सभी के Volume, TSA, CSA, क्षेत्रफल आदि सभी के बारे मे आपको इस Mensuration PDF मे दिया है।

All Mensuration Formula in English PDF	CLICK HERE
All Mensuration Formula in Hindi PDF	CLICK HERE

तो आपको यह जानकारी All Mensuration Formula In Hindi & English कैसी लगी नीचे कमेंट करके जरूर बताए, और यह जानकारी आपकी सभी परीक्षाओं जैसे class 6,7, 8, 9, 10, 11, 12 के साथ, SSC, Bank, Railway, UPTET, B.Ed, जैसी कई one Day exam मे मदद करेगी। इस पोस्ट को अपने दोस्तों मे शेयर जरूर करें।